2 things I find whacky about LLMs (coming from a statistical learning background)
Double Descent
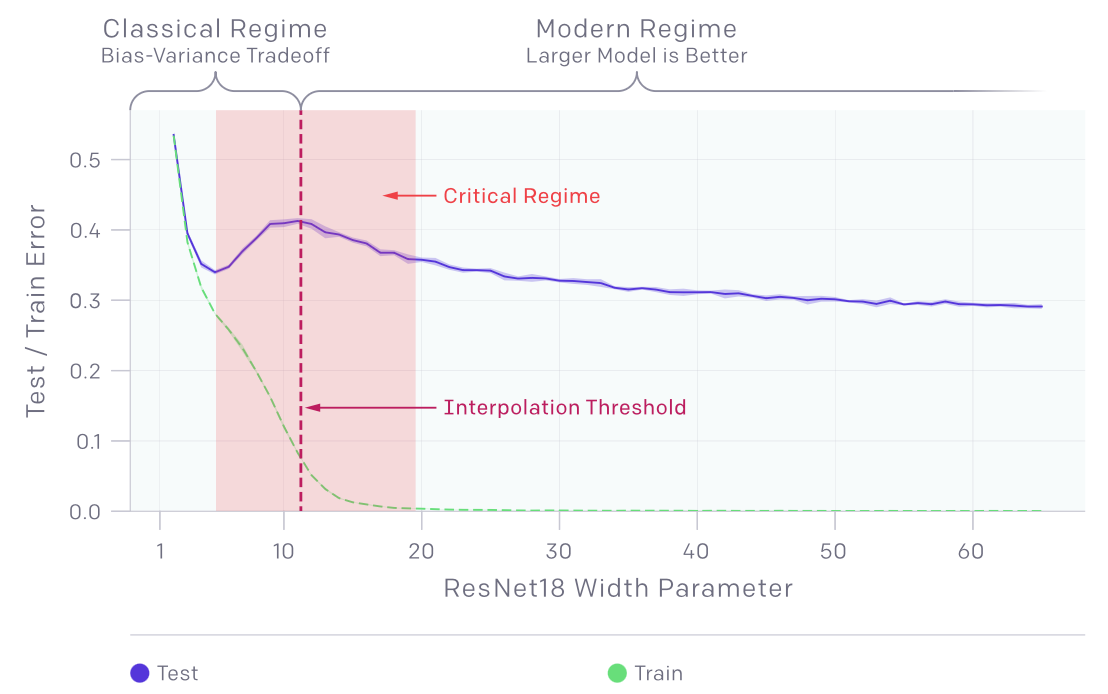
The double descent phenomenon suggests that models no longer overfit; instead, the test error continues to decrease even after crossing the critical region. This is clearly illustrated by OpenAI's diagram.
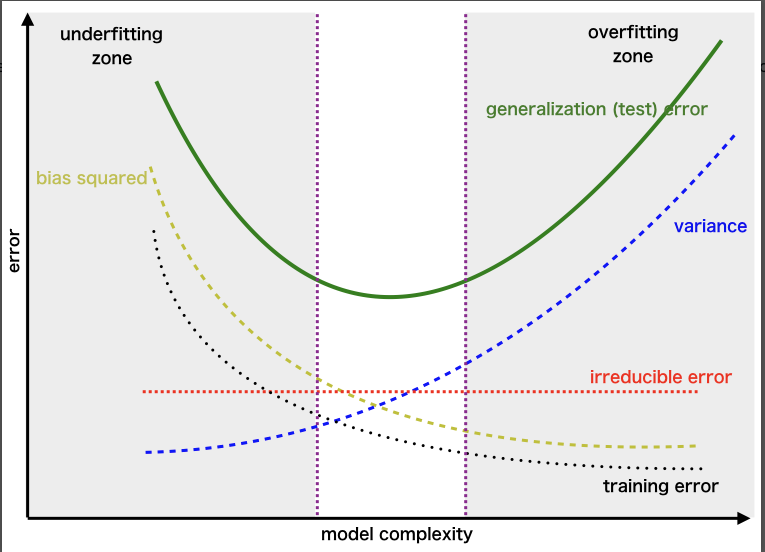
Having started my machine learning journey in the 2000s, prior to the success of AlexNet, my first, formal ML education is rooted in statistical learning theory. A core principle of this theory is the bias-variance tradeoff: the necessity of balancing models that are too simple (high bias) with those that overfit the training data (high variance).
The double descent phenomenon reveals two distinct regimes: a "classical" regime, where the bias-variance tradeoff applies to smaller models, and a "modern" regime, where larger models consistently exhibit superior performance. This parallels the relationship between classical and quantum mechanics in physics, where quantum physics governs the subatomic realm, while Newtonian physics applies to larger objects.
Curriculum Learning
Another intriguing concept is curriculum learning, which emphasizes the importance of the order of training data. This approach begins with "easier" examples and progressively increases difficulty, contrasting with statistical learning theory's emphasis on randomizing training data order.
While not a new concept—it was first introduced by Yoshua Bengio in his 2009 ICML paper, "Curriculum Learning," demonstrating improved training and generalization through meaningful organization of training samples from easy to difficult—I've recently heard from LLM researchers that curriculum learning is crucial for the pre-training of LLMs and foundational models.